

Obtained from it are likely to be unreliable. Why do we need to evaluate the precision of a measurement system? IfĪ system is not both accurate and precise, any conclusions based on data Of the bias observed when different operators measure the same parts

When a gage repeatability and reproducibility The interaction between the operatorĪnd part can also produce variation (e.g., some operators may be able to Variation due to the part, variation due to the measuring device (or gage)Īnd variation due to the operator. Within a measurement system, there are three basic sources of variation: In thisĪrticle, we will demonstrate how to use DOE++ to examine precision. Same part is measured repeatedly using the same measuring device). (i.e., the variation in measurements that can be expected when the Of a measuring device, and the gage R&R folio is used to study its precision
These tools, the linearity and bias folio is used to study the accuracy And the proposed model is compared with the standard Gage R&R model.Now provides a set of tools for measurement systems analysis. The variance component estimates are derived by setting the EMS equations equal to the corresponding mean square from the ANOVA table and solving.
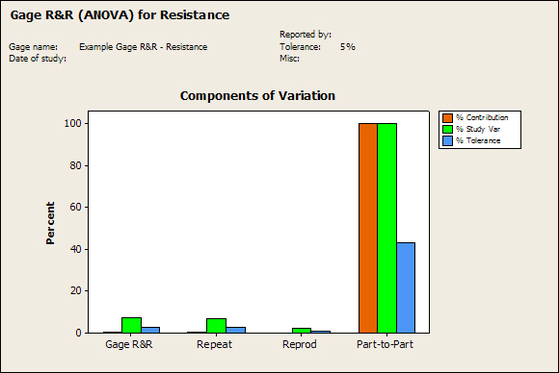
This paper presents a four-factor nested factorial ANOVA model which explicitly considers these variations for the Gage R&R study. That is, in the standard Gage R&R study these variations affect the estimate of repeatability, reproducibility, or both. However, if the process variation possesses the between group variation, within group variation, and within-part variation, these variations can cause the measurement system evaluation to provide misleading results. Then, the ANOVA partitions the total variation into three categories: repeatability, reproducibility, part variation. A typical ANOVA model used in a standard Gage R&R study is the two-factor random effect model. The sources of variation associated with the measurement system are compared using an analysis of variance (ANOVA) model, in general. If the measurement system variation is small relative to the process variation, then the measurement system is deemed 'adequate'. The purpose of the Gage R&R study is to determine whether a measurement system is adequate for monitoring a process.


 0 kommentar(er)
0 kommentar(er)
